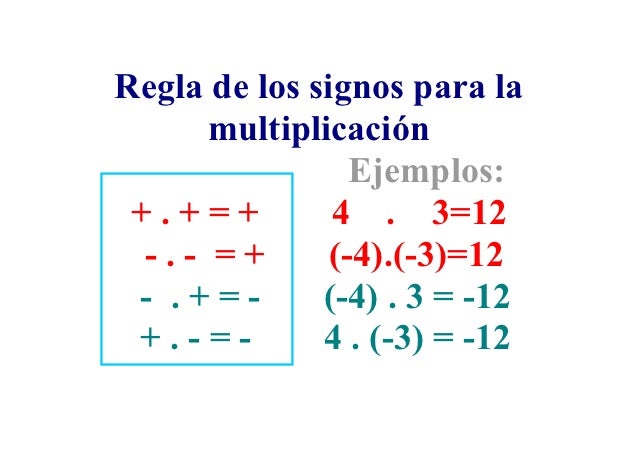
Se utiliza cuando el problema trata de dos magnitudes directamente proporcionales. Se aplicará cuando se establezcan las siguientes relaciones entre las magnitudes:
Matemática Básico en Vacaciones
miércoles, 27 de noviembre de 2019
domingo, 24 de noviembre de 2019
jueves, 21 de noviembre de 2019
Suma y Resta Algebraica
A la suma y resta algebraica se le llama REDUCCIÓN DE TÉRMINOS SEMEJANTES.
Se operan únicamente los términos que son semejantes entre si.
Los TÉRMINOS SEMEJANTES son aquellos que tiene la misma parte literal y los mismos exponentes, exactamente en la misma posición.




EJERCICIO:
martes, 19 de noviembre de 2019
Algebra





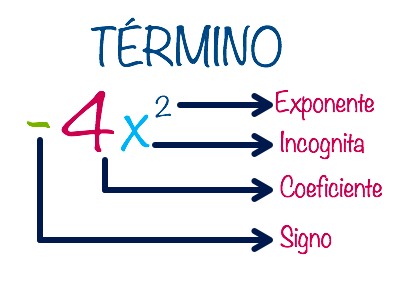

Reducir dos o más términos semejantes significa sumar o restar los coeficientes de los términos, dependiendo del signo, transformándolo en un solo término.
Ejemplo:
1. 9x + 7x + 3x = 19x
2. 13x - 7x = 6x
Reducir los siguientes términos semejantes:
1. 3x + 2x + x - 5x + (3x - 2x - x)
2. 4a + (7a - a + 5a)
3. -2x - (3x + 2x - x) + 8x
4. -4y3 - [2y3 + y3 + (3y3 - 4y3 )]
5. -3z - {-2x + 8z} + [8x - 5m + 9z] - 15x
6. - { - [3a + 6x - (2m - 5x)] - [-5z - 8m + 6a - (7x - 6m)]}
7. 2x3 - {3x3 + 5x - (2x3 + x3 - 3x)} - [5x3 - x + (2x - 3x3 + x)]
8. [a + b + (2a - 3b)] + [5b - 4a - (3b - 7a)]
domingo, 17 de noviembre de 2019
Tanto por ciento



Desde la aparición del hombre, mucho antes de que aprendiera
a pensar de si mismo, a razonar o a tener siquiera el primer concepto,
todo lo que le rodeaba le hablaba ya de matemáticas. El número de
plantas, la distancia de su cueva al río, el tamaño de la presa que debía
atrapar, el grupo formado por un conjunto de mamuts, la altura para coger los
frutos, la comparación de la rapidez entre los animales que debía atrapar, el
lapso entre la noche y el amanecer, el transcurrir de los días, el crecimiento
de su tribu, todo lo que le rodeaba no hacia sino conducirlo por un camino
incipiente e inevitable de la matemática: el de comparar, agrupar y
contar, la escena de un escarabajo que amasa pelotitas de estiércol quizá le
sugirió que la forma esférica en la más adecuada para hacer rodar y transportar
cuerpos.
De la araña que teje su tela para capturar sus presas
posiblemente aprendió a tejer fibras, construyendo redes adecuadas para
capturar sus alimentos, etc.
Así vació la matemática junto con el hombre, no porque el
hombre lo inventará, sino por sus necesidades propias y porque el lenguaje de
la naturaleza esta dado en conceptos de relaciones y funciones matemáticas.Por
eso debemos tener en cuenta, que las matemáticas tienen su aplicación en la
vida diaria.
² CONCEPTO
Es una o más
partes bañadas de las 100 partes en que se ha dividido un número.
4 x 100 = 4
por ciento = 4%
7 x 100 = 7
por ciento = 7%
En general:
A% de N = x N
Nomenclatura:
a% de N = R
P = porcentaje
N = número
R =
resultado
Casos Básicos
I. P % N = ?
Hallar el 15% de 200
Sol:
II. P% ? = R
El 20% de que número es 60.
Sol:
viernes, 15 de noviembre de 2019
Regla de Tres

DEFINICIONES
1. Regla de tres directa:
A más ➜ más
A menos ➜ menos
Directa – Ejemplo número 1:
8 es a … como 12 es a 48.
- 24
- 32
- 36
- 6
Se expresaría de la siguiente manera teniendo en cuenta que “es a” sería la línea que une la regla de tres. Al ser directa se resolvería de la siguiente manera:

Expresamos la regla de tres directa dividiendo lo de arriba entre lo de abajo y, al ser una regla de tres, se resuelve en cruz.
La respuesta correcta sería la B
2. Regla de tres inversa:
Se utiliza cuando el problema trata de dos magnitudes inversamente proporcionales. Se aplicará cuando se establezcan las siguientes relaciones entre las magnitudes:
A más ➜ menos
A menos ➜ más
Inversa – Ejemplo número 1:
Una treintena de soldados cavan una trinchera en cinco días. ¿Cuántos días tardarán quince soldados en cavar el mismo agujero?
- 10 días
- 2,5 días
- 5 dias
- 7,5 días
Lo primero que tenemos que hacer es colocar los diferentes conceptos que nos dan (soldados y tiempo). Después, tenemos que pensar que a más soldados que estén trabajando menos van a tardar. Como un concepto aumenta (soldados) y el otro disminuye (tiempo), sería una regla de tres inversa.

En este caso tenemos menos soldados, así que nos tiene que salir más días. La mejor forma de colocar la regla de tres inversa es de la siguiente manera: el lado que tiene x no lo tocamos nunca. Por lo tanto, tendríamos que dar la vuelta a la otra fracción. Después, se resuelve en cruz.
La respuesta correcta sería la A
EJERCICIO
Resolver dejando constancia de sus procedimientos. Subraye su respuesta final.
- Con cuarenta horas semanales de trabajo, un trabajador ganó $12000, ¿cuánto ganará si la semana siguiente puede trabajar cincuenta horas?
- Una motocicleta recorre 320 kilómetros en 150 minutos, ¿a cuántos kilómetros por hora viajó?
- Este año hubo 42 días con lluvias, ¿qué porcentaje del año significa eso?
- En 50 litros de agua de mar hay 1300 gramos de sal, ¿en cuántos litros estarán contenidos 11600 gramos?
- Una máquina fabrica 1200 tornillos en seis horas, ¿cuánto tiempo le llevará a la máquina fabricar 10000 tornillos?
- Si una persona puede vivir en Nueva York durante 10 días con 650 dólares. ¿Cuántos días podrá costearse si solo tiene 500 dólares?
- Con 5 litros de pintura se han pintado 90 m de verja. Calcular cuántos metros de verja se podrán pintar con 30 litros.
- Tres canillas tardan 10 horas en llenar un depósito de agua. ¿Cuántas horas tardarán 5 canillas en hacerlo?
- Si debo sembrar 30 semillas de maíz por surco, ¿Cuántos semillas necesitaré para dejar sembrado un lote de 20 surcos?
- Si en dos horas y media un motociclista ha cubierto una distancia de 320 kilómetros. ¿Ha superado el límite de velocidad previsto, que es de 80 km/h?
martes, 12 de noviembre de 2019
La potenciación


La jerarquía de las operaciones combinadas con potencias es la misma que la de los números naturales.
Lo recordamos:
- Paréntesis
- Multiplicaciones y divisiones
- Sumas y restas
- Si la jerarquía es la misma, las operaciones se realizan de izquierda a derecha
Una vez estudiada la teoría ya podemos resolver los ejercicios.
Ejercicio 1
Expresa con una sola potencia
a) 54 · 58
b) 126 · 123
c) 43 · 43 · 4
d) 77 · 72 · 74
Ejercicio 2
Expresa con una sola potencia
a) 78 : 73
b) 119 : 119
c) 28 : 2
d) 37 : 34
Ejercicio 3
Reduce a una sola potencia
a) 25 · 45
b) 73 · 93
c) ( 34 )5
d) ( 23 )6
Ejercicio 4
Reduce
a) x5 · x2 : x4
b) ( x2 )5 : ( x3 )2
c) ( 3 · 2 )4 ·( 3· 2)5
d) ( 5 · 2 )7 ·( 5· 2)4
Ejercicio 5
Expresa como una sola potencia
a) 27 : 25 · 24
b) 710 : 74 · 74
c) 1112 : (116 · 113)
d) 49 ·(47 : 43)
RESPUESTAS
Ejercicio 1
Expresa con una sola potencia
a) 54 · 58 = 512
b) 126 · 123 = 129
c) 43 · 43 · 4 = 47 ( ¡No te olvides del exponente 1! Recuerda que no se pone pero está ahí )
d) 77 · 72 · 74 = 713
En todos los casos hemos aplicado la propiedad am · an = a (m+n)
Ejercicio 2
Expresa con una sola potencia
a) 78 : 73 = 75
b) 119 : 119 = 110 = 1
c) 28 : 2 = 27
d) 37 : 34 = 33
Si no te has aprendido bien la propiedad que has aplicado, escríbela, tal y como he hecho en el ejercicio anterior. Si ya te la sabes, puedes escribirla para repasar.
Ejercicio 3
Reduce a una sola potencia
a) 25 · 45 = 85
b) 73 · 93 = 633
c) ( 34 )5= 320
d) ( 23 )6 = 218
Ejercicio 4
Reduce
a) x5 · x2 : x4 = x7 : x4 = x3
b) ( x2 )5 : ( x3 )2 = x10 : x6 = x4
c) ( 3 · 2 )4 ·( 3· 2)5 = 64 · 65 = 69
d) ( 5 · 2 )7 ·( 5· 2)4 = 107 · 104 = 1011
Ejercicio 5
Expresa como una sola potencia.
a) 27 : 25 · 24 = 22· 24 = 26
b) 710 : 74 · 74 = 76· 74 = 710
c) 1112 : (116 ·113) = 1112 : 119 = 113
d)49 · (47 : 43) = 49 · 44 = 413
Suscribirse a:
Comentarios (Atom)